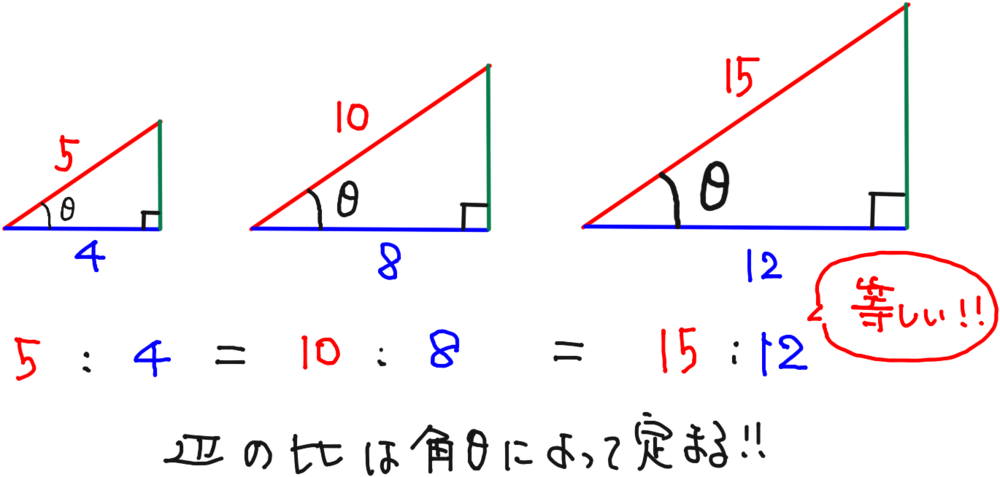【読んで理解】三角比の定義
「三角比、教えてくれ。」
「相変わらず唐突だね。」
「唐突も何もあるかいな。俺が三角比を学びたいと思った。目の前には数学得意マンのお前がおる。じゃあ発する言葉は『三角比、教えてくれ。』の一択やろ。」
「大きなものの高さを測るとしたら、どうする？」
「相変わらず唐突やな。」
「きみに『三角比、教えてくれ。』って言われたら、いつものように『三角比とはなんぞや？』ということを聞いてるんだろうなーという推測がたつ。じゃあ僕が発する言葉はいくつかの選択肢があったけど、『大きなものの高さを測るとしたら、どうする？』でいこうと思っただけだよ。」
「そんなもんか。で、大きなものの高さを測るってどゆこと？」
「例えば、こんな図が与えられたとしよう。
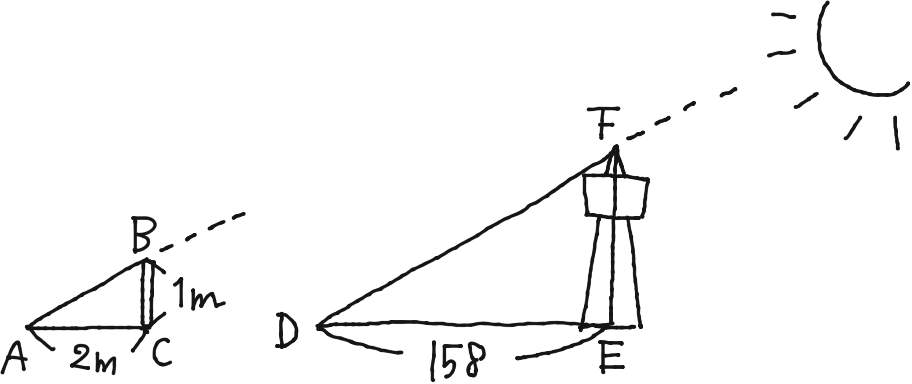
このときの、塔の高さ$EF$は何mでしょう？って感じかな。」
「これは、、、簡単なんちゃうか？図の中の$\triangle ABC$と$\triangle DEF$は相似になってること利用したらいけるやん。
$2:1=158:EF$
が成り立つから、それ利用して、塔の高さは$79$m。」
「正解！」
「これくらいできるっちゅーねん。で、これと三角比になんの関係があるん？」
「これこそ、三角比の出発点だよ。」
直角三角形の角と辺の比
「そうなん？」
「そう。じゃあ実際に三角比の話に入っていくね。
3つの直角三角形があるとする。
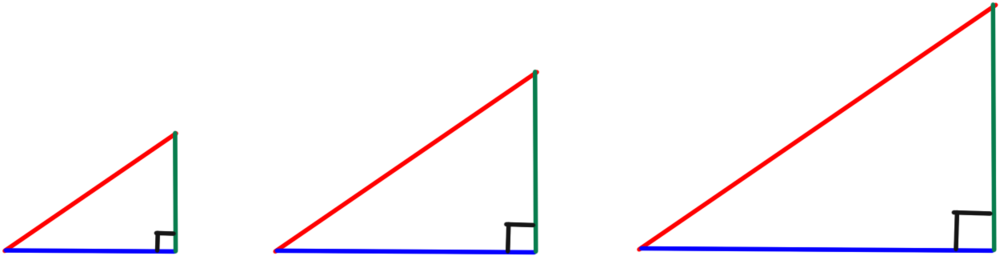
今、3つの直角三角形の左側の角の大きさを全て同じ$\theta$であるとしようか。
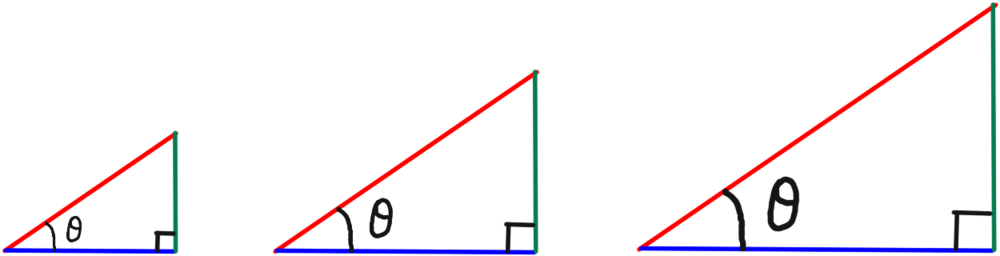
じゃあどうなる？」
「3つの直角三角形は相似やわな。」
「そうだよね。『二つの角がそれぞれ等しい』から、相似になる。」
いくつか直角三角形があり、直角以外の角のどちらか一つが等しければ、それらの直角三角形はすべて相似
「んで？」
「この3つの直角三角形は全て相似で、角の大きさも等しい。
じゃあここで辺の長さを書き込んでみる。
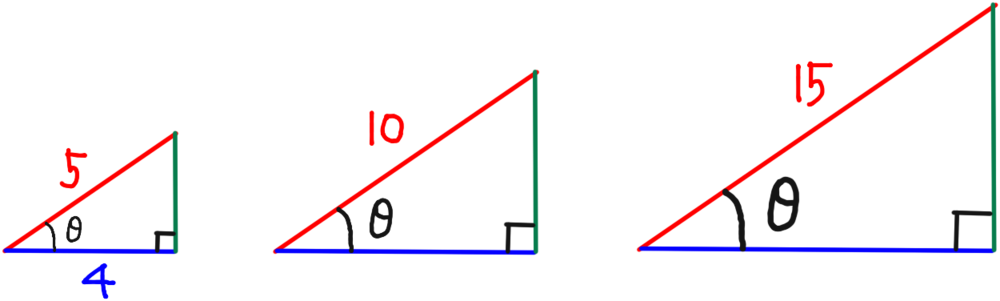
一番左の三角形の辺がわかってるわけだけど、他の2つの直角三角形の辺の大きさはどうなる？」
「3つの直角三角形は相似やから、真ん中の三角形の底辺の大きさは$8$で、右の三角形の底辺の大きさは$12$ってことがわかるな。さっきの塔の高さ求めるときと一緒やん。」
「そうそう。他の三角形の1つの辺がわかってたら、相似であることを利用して他の辺の長さも求めることができる。
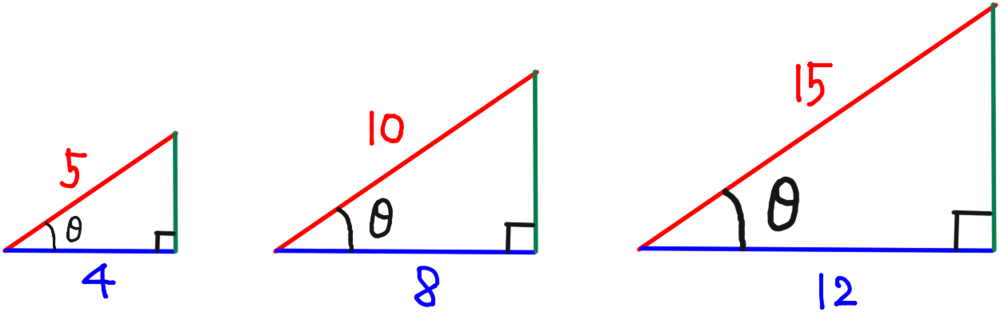
つまり、相似な関係にある三角形の各辺の比は、それぞれ等しい。」
「せやな。」
「じゃあここまでで、3つの三角形においてわかったことをまとめておこう。」
・左側の角の大きさは全て$\theta$
・各辺の比はそれぞれ等しく、$5:4=10:8=15:12$が成り立つ
「うん。」
「つまり、どんな直角三角形においても、左側の角度が同じであれば、相似な関係となり、辺どうしの比が等しくなる、ってことがわかった。
これって、『左側の角の大きさを$\theta$と定める』と、『各辺の比は一つの値に定まる』ってことだよね。」
「どんな直角三角形を考えても、左側の角の大きさが$\theta$で同じなら、それらの直角三角形の辺の比は等しくなるってことか。」
「そのとおり！」
「ふむふむ。で、、、三角比まだ？」
「もう出てきてるよ。」
「ん？どこに？」
「直角三角形の、角$\theta$によって定まる各辺の比は常に等しい。
つまり、角$\theta$を定めると各辺の比が定まる。
この、角$\theta$によって定まる各辺の比のことを三角比っていうんだ。」
比と分数
「え？そうなん？」
「うん、そうだよ。
ところで、比って分数で、分数って比だよね？」
「比は分数で分数は比、、、なんか？『$r:x=5:3$』とかが比じゃないん？」
「うん、「比」って言われるとそんな風に表されたものを考えるけど、
$r:x=5:3$
から
$5x=3r$
両辺を$5r$で割ると、
$\displaystyle\frac{x}{r}=\displaystyle\frac{3}{5}$
という風に、$r:x=5:3$という式と、$\displaystyle\frac{x}{r}=\displaystyle\frac{3}{5}$は同じ。だから、比は分数で表すことができるし、分数は比で表すことができる。」
$r:x=5:3 \Leftrightarrow \displaystyle\frac{x}{r}=\displaystyle\frac{3}{5}$
「なるほど。比は分数で表すことができ、分数は比で表すことができるわけやな。」
三角比の定義
「んでえーと、、、俺らはなんの話をしてるんやったっけ？」
「『三角比とは何か？』というところからスタートして、
『直角三角形の、角$\theta$によって定まる各辺の比は常に等しい』
ってことと、、、」
「『比は分数で表すことができ、分数は比で表すことができる』のんを確認したんか。」
「そうそう。
『直角三角形の、角$\theta$によって定まる各辺の比は常に等しい』
『比は分数で表すことができる』
だから、
『直角三角形の直角以外の角$\theta$で定まる辺どうしの比』を分数で表して、それに名前をつけたものが三角比なんだ。」
「どんな直角三角形考えてみても、直角以外の角が等しいければ、それらの直角三角形の辺の比は全て同じになる。
同じ値をとるならそいつに名前つけて考えていこ、ってわけか。」
「そういうことになるね。 辺の比は$\theta$によって1つに決まるので、$\theta$と辺の比との対応に『サイン』『コサイン』『タンジェント』と名付けることにした。
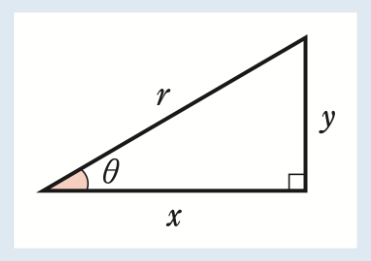
名付けることにした比は3つ。
- $\displaystyle\frac{y}{r}$：斜辺と縦の長さの比
- $\displaystyle\frac{x}{r}$：斜辺と横の長さの比
- $\displaystyle\frac{y}{x}$：横の長さと縦の長さの比
これらと、$\theta$との対応に名前をつけるわけだから、$\theta$を用いて
- $\sin\theta=\displaystyle\frac{y}{r}$（斜辺と縦の長さの比を$\sin\theta$）
- $\cos\theta=\displaystyle\frac{x}{r}$（斜辺と横の長さの比を$\cos\theta$）
- $\tan\theta=\displaystyle\frac{y}{x}$（横の長さと縦の長さの比を$\tan\theta$）
というふうに名付け、定めた。これが三角比の"定義"。『三角比って何か？』という問いへの答えだね。
三角比はここからスタートする。この定義から。そしてこの後、いろんな性質や定理が導かれていくことになる。この三角比の定義は、三角比を学ぶうえで当たり前だけど無茶苦茶大事、ということになってくる。」
「この先のこともちょろっと見たけど、なんか色々出てくるでなぁ。こうやって定義されてるってのはわかったけど、『。。。で？』感が否めへんな。」
「うん。でも何かの定義ってそんなものじゃないかな。定義されたときには、それがなんの意味を持つのか、どういう意義があるのかは僕たちにはまだわからない。定義を、定めたことをスタートとしてあれこれ考えていくことで、その有用さとか強力さとか広がりがわかってくるわけだから。」
「まぁ、そんなもんか。」
「しかし、いつも悪いな。あれこれ聞くたんびに丁寧に教えてくれて。でもまぁ、また頼むわ。」