【読んで理解】三角比の拡張
きりーつ、
れーい、
ちゃくせーき。
「ほしたらはじめていきましょうかいね。
前回、これから三角関数を学んでいくにあたって、三角比の復習をやったと思います。
数学Ⅰのほうで三角比ってのを学んだわけやけど、いちばんはじめにこんな風に定義されてたんを思い出してもらったわけやね(【読んで理解】三角比の定義)。

で、これやった後に、この定義やとθとして90∘までしか考えられんから、180∘までsinθ, cosθ, tanθの値を定義できるようにしよう、って習ってるんやけど、覚えてる?
いいねぇ、その『そんなんやったっけ?』ってのが滲み出てるみんなの顔。まぁ無理もないっちゃ無理もない。1年くらい前に学んだことやからね。そんときに強烈に記憶に残ってないと、1年経ったらなかなか覚えてへんよ。
きっとこんな図かいて考えたと思うんやけど、こんとき疑問に思えへんかった?
『なんで180∘までなん?』
って。角度ってもっと大きいものまで考えれるやん。200∘とか350∘とか。やのに何で180∘までなんや、と。
その疑問はもっともで、別にまったく180∘までと限定する必要はない。
今日はその疑問に答えていくってのがメインの話。
でな、この、三角比の角θがどんな大きさでもsinθ, cosθ, tanθの値を考えれるようにする話が、俺の記憶には強烈に残ってるねん。今でもそん時のことを思い出せるくらいに。」
「前、唐突に『三角比、教えてくれ。』ってきみがいうから、直角三角形による三角比の定義を教えたけど、あの定義ってなんであの形なんだろう、と思ったりしない?」
「どゆこと?あぁ定められてるから、それ以上のことないんちゃうの?」
「いや、そんなこともないよな、と思って。
三角比、覚えてる?」「んーと、大きさの違う直角三角形であっても、直角以外の角が同じであれば、辺の比はすべて同じになり、1つに決まる。やから、角によって決まる辺の比に、sinθ, cosθ, tanθって名前つけたって話やったよな?」
「完璧!」
「うん、ちゃんとあの後復習して、簡単な三角比の問題も解いたりしたもん。」
「さすがだね。」
「お前を見習ってるだけや。これでも数学けっこう好きやからね。」
「でね、直角以外の角が等しい直角三角形はみんな相似になるのに、なんで毎回斜辺と縦の比でyrだなーとか考えるんだろうと思って。」
「えーと、どゆこと?今のついていけてない。おいていかんといて。」
「例えば、、、相似だったら、次の図のどの直角三角形で比を考えてもいいよね。」
「うん。」
「もっと言うと、ここに書いてない直角三角形を考えて、その比を考えてもいい。」
「。。。せやな。ここに書いてるのと相似な直角三角形考えたらいけるわな。」
「うんうん。それなら、都合のいい三角形を考えちゃえばいいと思わない?」
「都合のいい三角形。。。」
「sinθやcosθの値がわかりやすいような。」
「。。。」
「しゃ、、」
「ちょっと待て待て、待ってや。わかりそうやから考えさせて。
相似な三角形の辺の比は等しい。
辺の比が等しいから、相似な三角形のうちどれを考えてもいい。
どの直角三角形でもえぇなら、sinθやcosθを考えやすい、都合のいい直角三角形をもってきたらいい。
ってことか!」「そうそう!」
「で、都合のいい直角三角形ってどんなんか考えてみると、、、sinθ=yrで、これが考えやすいっつったら、、斜辺の大きさが1の直角三角形、、、か!
斜辺が1の直角三角形考えたら、縦の大きさが
yr=sinθになるし、横の大きさが
xr=cosθになる。。。!」「そうそう!『斜辺ぶんの縦』とか『斜辺ぶんの横』とか考えなくても、斜辺が1の直角三角形を考えてあげれば。。。」
「その縦の大きさがsinθ、横の大きさがcosθや!」
「そう!だから、斜辺が1の直角三角形の縦の大きさをsinθ、横の大きさをcosθと定義してしまえばいい!」
「!!!定義してまえばいいの!?そんなんしてえぇの?」
「いいよ、きっと。だって定めてる値は同じだもん。」
「その、強烈に残ってるのをちょっとでもみんなに強烈に伝えることができればな、と思うねんけど、そこはまぁどうやろなぁ。力量が試されるわけやけど、なかなか自信はないが。
ほなやっていこう。
三角比は直角三角形を用いて定義された。
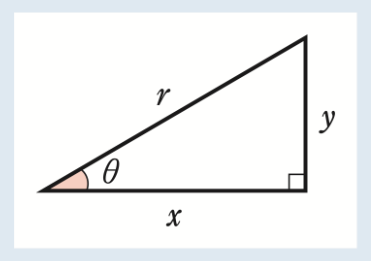
- sinθ=yr(斜辺と縦の長さの比をsinθ)
- cosθ=xr(斜辺と横の長さの比をcosθ)
- tanθ=yx(横の長さと縦の長さの比をtanθ)
ここで、ちょっといろんな直角三角形を書いてみるで。
これらの直角三角形は、どんな関係にあるか?相似やでな。
相似やから、すべての直角三角形の各辺の比は等しい。からその比にsinθ, cosθ, tanθと名付けよう、って話やったわけや。
つまり、これらの直角三角形においてsinθ, cosθ, tanθの値は等しくなるねんから、どの直角三角形でsinθ, cosθ, tanθを考えて定めても、なんの問題はないってことやんな。
ほしたらみんなやったらどの直角三角形で考えていくんが楽そうというか、考えるときに都合良さそうやと思う?
それぞれの辺を求めておくと、、、
とりあえず、約分はせんで済む方がえぇでな。やから一番右の直角三角形はボツ。
今考えてるのは、sinθやcosθを求めるときに都合良さそうな直角三角形。
、、、それってこれちゃう?斜辺が1の直角三角形。
だって、この直角三角形の縦の大きさってsinθやし、横の大きさってcosθやん。
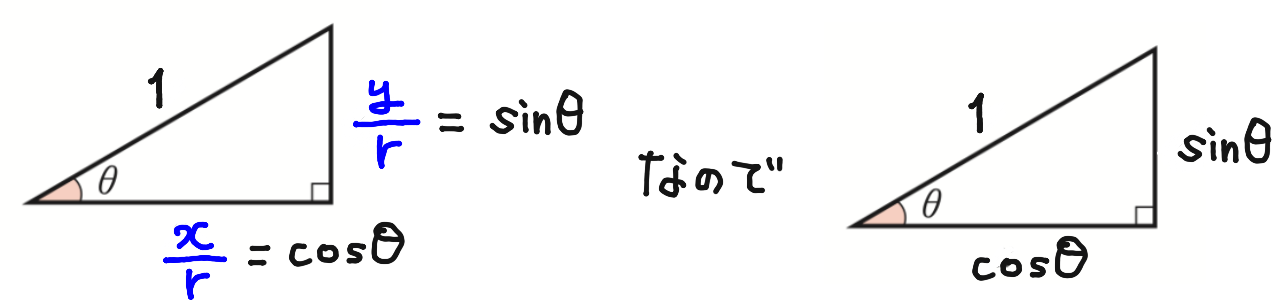
いちいち斜辺と縦でsinθ、、、とか考えんくてよくて、斜辺の大きさが1なら、「縦の大きさがsinθ」って考えれるやん。
で、今考えたかったんは、θが90∘以上においてもsinθ, cosθ, tanθを考えれるようにすることやった。
そこで、この直角三角形をxy平面に置いてみる。
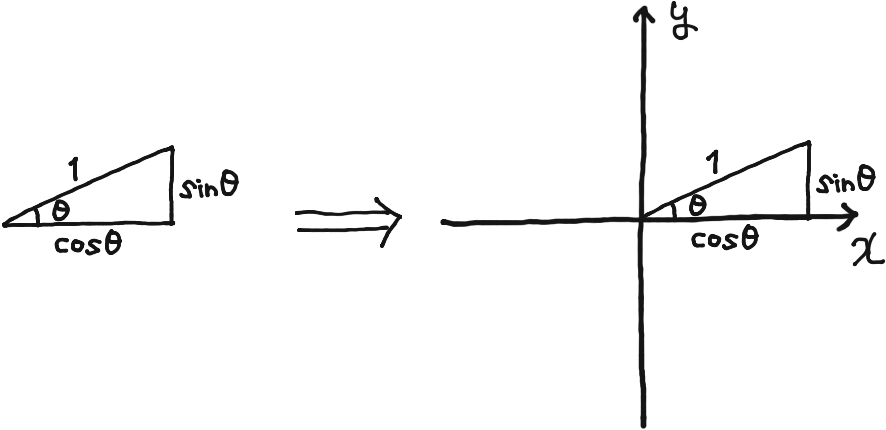
θのある頂点をxy平面の原点の上に置いて、直角はx軸の上に。
そしたら、直角三角形の縦の大きさがsinθ、横の大きさがcosθやから、右上の、θでも直角でもない角の頂点の座標が(cosθ, sinθ)となってることがわかる。
直角三角形の頂点でx軸上にないものの座標が(cosθ, sinθ)やということ。
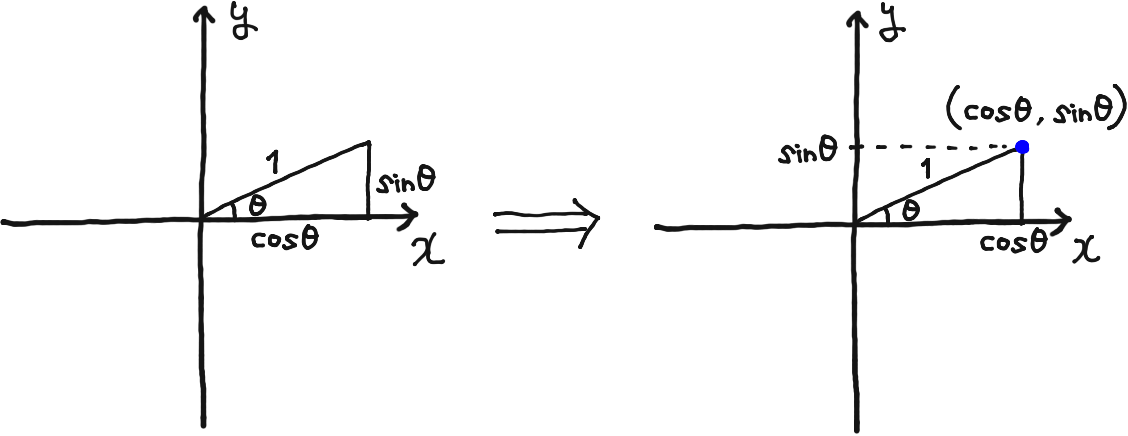
で、θは、x軸と直角三角形の斜辺とのなす角になってるな。
こっからθの大きさを90∘以上においても考えれるようにしていくでー、というか、ほぼもうできてると言えるねんけども。
とりあえずθの大きさをいろいろ考えてみよか。いっぱい書いてみるで。
直角三角形をxy平面に置いて考えて、x軸上にない頂点の座標を(cosθ, sinθ)と定めた。で、x軸と斜辺のなす角がθとなってる。
このx軸上にない頂点は、仮にθの大きさを90∘以上にしていった場合、どんな風に変化していくか。図の青い点は、θを変化させることで、どんな風に動いていくやろう?
そう!円を描く!!
ここに描いてる直角三角形は全て斜辺の大きさが1やから、円の半径は1。
ってことは、半径1の円上の点の座標を(cosθ, sinθ)と定義すれば、90∘以上の角の大きさについても、sinθとcosθの値を定めることができる、ということになる!
- 図における青い点の座標を(cosθ, sinθ)と定める
- 青い点は、θの大きさを変化させると、円を描く
- よって、円上の青い点のx座標をcosθ、y座標をsinθとおくことで、90∘以上の角においてもcosθとsinθの値を考えることができる
直角三角形ではsinθとcosθの値はプラスの値しかとらへんかったけど、「円上の点」を用いてsinθとcosθを定めると、マイナスの値をとり得ることがわかる思う。
左の図においては、x座標と定めたcosθの値はマイナスになる。y座標と定めたsinθの値はプラス。
ほしたら右の図においてはどうやろう?円上の点のx座標がcosθ、y座標はsinθであることを元に考えると、、、cosθの値もsinθの値もマイナスになるでな!
んで、一つ忘れられてるやつおるでな。tanθ。こいつはどうするか。
tanθ=yx(横の長さと縦の長さの比)やった。で、斜辺が1の大きさの直角三角形においては、縦の大きさがsinθ、横の大きさがcosθ。ってことは、斜辺が1やったらtanθ=sinθcosθになる。これをそのまま円においても考えちゃえばいい。
半径が1の円上の点の
- x座標=cosθ
- y座標=sinθ
と定義し、tanθは
- tanθ=sinθcosθ
と定義する。そしたら、「どんな大きさの角θにおいても、sinθ, cosθ, tanθの値を定める」ことができる、ってわけやな。」
「なぁなぁ」
「ん?」
「原点が中心の半径1の円上の点のx座標をcosθ、y座標をsinθと定義することで90∘以上のθにおいてもsinθ, cosθ, tanθの値を定めることができたわけやけど、」
「うん。」
「これってあの、sinθとcosθに対して成り立ってた式も同じように成り立つの?
あの、cos2θ+sin2θ=1ってやつ。」「。。。気になるなら、確かめてみたら?」
「むむむ。」